Question

A gas has a volume of 0.50 L, a pressure of 0.5 atm, and a temperature of 40°C. What will be the new temperature if the gas is expanded to 5.0 L and a pressure of 0.10 atm?

Answer 1

626.3K or 353.15°C

Step-by-step explanation:

We will be using the Combined Gas Law for this problem. The Combined Gas Law (as you guessed it!) combines Boyle's Law, Charles' Law, and Gay-Lussac's Law into a single equation for situations where P, V, and T all vary. It expresses the relationship between pressure, volume, and temperature of a fixed amount of gas. Remember, it allows calculations where only the amount of gas is constant.

Note: When using this law, temperature (T) MUST be in Kelvin Temperature. I can't stress how important it is to convert the temperature value into Kelvin degrees because forgetting to do so will mess up your answer.

Combined Gas Law:
`( P_(1)*V_(1))/(T_(1)) = ( P_(2)*V_(2))/(T_(2))`

In this problem, all of the values for the left side of the equation are given: P1 = 0.5 atm, V1 = 0.50L, and T1 = 40°C + 273.15 = 313.15K. For the right side of the equation, we are given the volume and pressure of the expanded gas and are told to find the new temperature (T2): P2 = 0.10 atm and V2 = 5.0L. Because the pressure and volume for both sides of the equations are provided in the same unit, there is no need for conversions.

Now onto the math - all that is needed to be done is plugging in the values and solving for T2. The work is shown below:

Set up:
`(0.5atm * 0.50L)/(313.15K) = (0.10atm * 5.0L)/(T_(2))`

==>
`((0.5atm * 0.50L)/(313.15K) )T_(2)= (0.10atm)(5.0L)`

==>
`T_(2)= (0.10atm) (5.0L)((313.15K)/((0.5atm)(0.50L)))`

==>
`T_(2) = 626.3K`

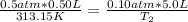
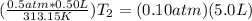
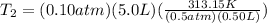
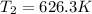
At this point, you can leave your answer as 626.3K. However, because the temperature of the original gas was given in Celsius, I would recommend converting it back to that provided unit. So, our final step is: 626.3K - 273.15 = 353.15°C.