We are given with a circle and we need to find the equation of the circle , but first let's recall that , the equation of a circle with radius 'r' and centre at (h,k) is given by
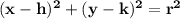
Now , here as as the circle cuts the +ve x-axis at (9,0) . So , it's radius is 9 units or the 2nd way is to measure the distance from centre of the circle to the point where the circle cuts the graph , as the centre is at Origin , so here (h,k) = (0,0) .Which means that the centre is located at the point whose coordinates are (0,0) which is also known as origin . Now , finding the equation of the circle :-
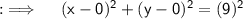
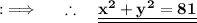
This is the required equation of Circle