Question

What are the integer solutions to the inequality below?


`3\leq 3x-4\ \textless \ 2x+1`

Answer 1

Given:

The compound inequality is:

`3\leq 3x-4<2x+1`

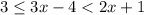
To find:

The integer solutions for the given compound inequality.

Solution:

We have,

`3\leq 3x-4<2x+1`

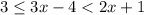
Case 1:
`3\leq 3x-4`

`3+4\leq 3x`

`(7)/(3)\leq x`

`2.33...\leq x` ...(i)

Case 2:
`3x-4<2x+1`

`3x-2x<1+4`

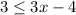
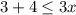
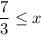
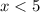`x<5` ...(ii)

Using (i) and (ii), we get

`2.33...<x<5`

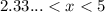
The integer values which satisfy this inequality are only 3 and 4.

Therefore, the integer solutions to the given inequality are 3 and 4.