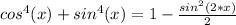Question

Prove that sin^4x + cos^4x= sinxcosx

Answer 1

(the relation you wrote is not correct, there may be something missing, so I will simplify the initial expression)

Here we have the equation:

`sin^4(x) + cos^4(x)`

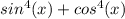
We can rewrite this as:

`(sin^2(x))^2 + (cos^2(x))^2`

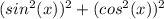
Now we can add and subtract cos^2(x)*sin^2(x) to get:

`(sin^2(x))^2 + (cos^2(x))^2 + 2*cos^2(x)*sin^2(x) - 2*cos^2(x)*sin^2(x)`

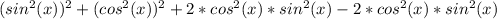
We can complete squares to get:

`(cos^2(x) + sin^2(x))^2 - 2*cos(x)^2*sin(x)^2`

and we know that:

cos^2(x) + sin^2(x) = 1

then:

`1 - 2*sin(x)^2*cos(x)^2`

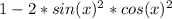
This is the closest expression to what you wrote.

We also know that:

sin(x)*cos(x) = (1/2)*sin(2*x)

If we replace that, we get:

`1 - (sin^2(2*x))/(2)`

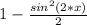
Then the simplification is:

`cos^4(x) + sin^4(x) = 1 - (sin^2(2*x))/(2)`