a) y = 9216
b) y = 360
Since x and y vary directly, y and x are directly related and can be expressed as y = kx. where k is a constant
y will increase as x increases. y will also decrease as x decreases.
I used k1 and k2 to separate the two questions and avoid confusion but using the constant k is fine.
a) For part a, you can substitute y = kx with the values of y and x.
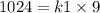
Hence, we can find the constant k1
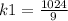
Now, we can plug in the values into the original equation and obtain the new equation
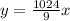
We can now solve part a by plugging in 81 into the value of x.
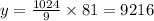
b) Like part a, we can use the same method to find y for part b.
substitute y = kx with the values of y and x.
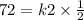
Hence, we can find the constant k2
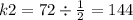
Now, we can plug in the values into the original equation and obtain the new equation
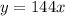
We can now solve part a by plugging in 5/2 into the value of x.
