Question

9-127 Nicole has three long logs. She wants to place them in a

triangle around a campfire to allow people to sit around the fire
The logs have lengers 9.11 and 21 feet
Can Nicole create a right triangle with the logs she has
Use the Pythagorean theorem to justify your answer

Answer 1

The logs do not form a right-angle triangle

Explanation:

Given

`Logs: 9ft, 11ft, 21ft`

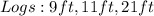
Required

Do the logs form a right-angled triangle

Applying Pythagoras theorem

`a^2 = b^2 + c^2`

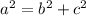
Where a is the length of the longest log.

So, we have:

`21^2 = 9^2 + 11^2`

`441 = 81 + 121`

`441 \\e 202`

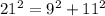
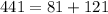
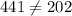
The above shows an inequality.

Hence, the logs do not form a right-angle triangle