Question

A vehicle factory manufactures cars. The unit cost C(the cost in dollars to make each car) depends on the number of cars made. If x cars are made, then the unit cost is given by the function C(x)=0.7x^2-420x+81,610. How many cars must be made to minimize the unit cost? Do not round your answer.

Answer 1

300 cars must be made to minimize the unit cost

Explanation:

Vertex of a quadratic function:

Suppose we have a quadratic function in the following format:

`f(x) = ax^(2) + bx + c`

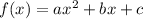
It's vertex is the point
`(x_(v), y_(v))`

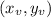
In which

`x_(v) = -(b)/(2a)`

`y_(v) = -(\Delta)/(4a)`

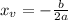
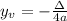
Where

`\Delta = b^2-4ac`

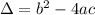
If a>0, the vertex is a minimum point, that is, the minimum value happens at
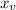`x_(v)`, and it's value is
`y_(v)`.

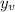The cost of producing x cars is given by:

`C(x) = 0.7x^2 - 420x + 81610`

So a quadratic equation with
`a = 0.7, b = -420, c = 81610`

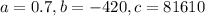
How many cars must be made to minimize the unit cost?

This is the xvalue of the vertex. So

`x_v = -(b)/(2a) = -(-420)/(2*0.7) = (420)/(1.4) = 300`

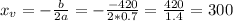
300 cars must be made to minimize the unit cost