Question

I WILL REWARD HIGHEST POSSIBLE THING, JUST ANSWER PLEASE!

Answer 1

Given:

Endpoints of a line segment EF are E(-3,8) and F(7,-7).

Point P divides the segment EF such that EP:PF = 2:3.

To find:

The coordinates of the point P.

Solution:

Section formula: If a point divides a line segment in m:n, then the coordinates of the points are:

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

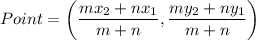
It is given that EP:PF = 2:3. It means the point P divides the segment EF in 2:3.

Using section formula, we get

`P=\left((2(7)+3(-3))/(2+3),(2(-7)+3(8))/(2+3)\right)`

`P=\left((14-9)/(5),(-14+24)/(5)\right)`

`P=\left((5)/(5),(10)/(5)\right)`

`P=\left(1,2\right)`

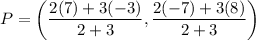
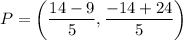
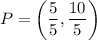
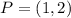
Therefore, the coordinates of the point P are (1,2).