Question

If one leg of a triangle is 6 inches and the hypotenuse is 13 inches, what

is the length of the other leg?

Answer 1

7 inches duhh

Explanation:

Answer 2

`\boxed {\boxed {\sf b \approx 11.53 \ in}}`

Explanation:

Since this is a right triangle, we can use the Pythagorean Theorem.

`a^2+b^2=c^2`

In this theorem, a and b are the legs and c is the hypotenuse.

We are given one leg that is 6 inches and the hypotenuse is 13 inches. We don't know the other leg. Substitute the known values into the formula.

`(6 \ in)^2+b^2=(13 \ in)^2`

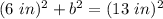
Solve the exponents.

• ( 6 in)²= 6 in* 6 in= 36 in²

`36 \ in^2+b^2=(13 \ in)^2`

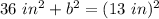
• (13 in)²= 13 in*13 in= 169 in²

`36 \ in^2+b^2=169 \ in^2`

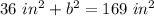
Now, solve for b (the unknown side) by isolating the variable. 36 square inches is being added. The inverse of addition is subtraction, so we subtract 36 from both sides.

`36 \ in^2-36 \ in^2+b^2=169 \ in^2- 36 \ in^2`

`b^2=169 \ in^2- 36 \ in^2`

`b^2=133 \ in^2`

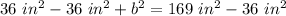
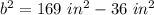
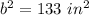
b is being squared. The inverse of a square is the square root. Take the square root of both sides.

`\sqrt {b^2}=\sqrt {133 \ in^2}\\`

`b=\sqrt {133 \ in^2}\\`

`b= 11.5325625947 \ in`

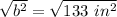
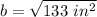
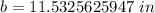
Let's round to the nearest hundredth. The 2 (11.5325625947) in the thousandth place tells us to leave the 3.

`b \approx 11.53 \ in`

The length of the other leg is approximately 11.53 inches.