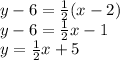Answer:
Explanation:
1) First, find the slope of the line that passes between the two points. Substitute the x and y values of (2,6) and (-8,1) into slope formula,
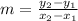 . Then, solve:
. Then, solve:
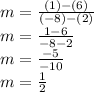
So, the slope is
 .
.
2) Now, write the equation of the line using the point-slope formula,
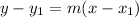 . Substitute real values for
. Substitute real values for
 ,
,
 , and
, and
 .
.
Since
 represents the slope, substitute
represents the slope, substitute
 in its place. Since
in its place. Since
 and
and
 represent the x and y values of a point the line intersects, substitute the x and y values of one of the given points into the formula as well. (Any of the two will do. Either choice will represent the same line. I chose (2,6).) Then, isolate y to put the equation in slope-intercept form and find an answer:
represent the x and y values of a point the line intersects, substitute the x and y values of one of the given points into the formula as well. (Any of the two will do. Either choice will represent the same line. I chose (2,6).) Then, isolate y to put the equation in slope-intercept form and find an answer: