Question

According to the graph on your graphing tool, what is true about f(x)= x^4-4x^2+x/-2x^4+18x^2

Answer 1

b,c,d

Explanation:

edg 21 ^u^

Answer 2

I can't see the options, so i will find all the asymptotes.

We have the function:

`f(x) = (x^4 - 4*x^2 + x)/(-2*x^4 + 18*x^2)`

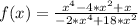
First, we can graph this using a graphing tool, the graph can be seen below.

In the graph, we can see that when we approach x = 0 from the left, f(x) goes to negative infinity, while if we approach x = 0 from the right, f(x) goes to infinity.

This can be written as:

`\lim_(x \to 0_-) f(x) = - \infty \\`

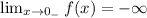
and:

`\lim_(x \to 0_+) f(x) = + \infty \\`

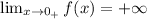
A similar thing can be seen at x = 3, when we approach from the left f(x) goes to infinity, while if we approach from the left, f(x) goes to negative infinity.

Then:

`\lim_(x \to 3_-) f(x) = \infty \\\\\lim_(x \to 3_+) f(x) = - \infty \\`

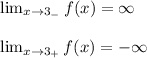
For x = -3 we can see that when we approach from the left, f(x) goes to negative infinity, while if we approach from the right, f(x) goes to infinity.

Then:

`\lim_(x \to -3_-) f(x) = - \infty \\\\\lim_(x \to -3_+) f(x) = + \infty \\`

We also can see that as x goes to negative infinity or positive infinity, f(x) tends to -0.5

Then:

`\lim_(x \to \infty) f(x) = -0.5 \\ \lim_(x \to -\infty) f(x) = -0.5`

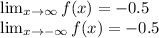
So you need to check the options that match with some of the given tendencies.