Answer:
(a) The amount owed At the end of 1 year is $3,815
(b) The amount owed At the end of 2 years is $4,158.35
Explanation:
The given parameters on the loan amount are;
The amount Salma borrows = $3,500
The interest rate at which the loan is borrowed, r = 9% compound interest annually
The assumption are that no payments are made out of the loan
(a) The formula for finding a compound interest loan amount, 'A' is given as follows;
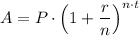
Where;
A = The amount owed
P = The principal (the initial amount borrowed)
r = The interest rate = 9% = 0.09
n = The number of times the interest is paid per unit period, 't' = 1
t = The number of periods of the loan = Number of years
At the end of 1 year, t = 1, we get;
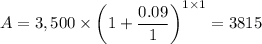
The amount owed, A = $3,815 at the end of 1 year
(b) The amount owed at the end oy 2 years is found by plugging in t = 2 years into the formula for finding the amount owed by the borrower, therefore, we get;
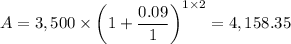
At the end of 2 years, the amount owed, A = $4,158.35