Question

Se tienen cuatro libros de Matemáticas, tres Biología y tres Religión ¿De cuántas maneras diferentes se pueden ordenar todos los libros en línea recta?

Answer 1

4,200

Explanation:

Tenemos un total de:

4 libros de matemáticas

3 libros de biología

3 libros de religión

10 libros en total.

Ahora vamos a contar la cantidad de opciones que tenemos para cada posicion.

Primer libro (tenemos 10 opciones)

segundo libro (tenemos 9 opciones, porque ya colocamos un libro)

tercer libro (tenemos 8 opciones, porque ya colocamos dos libros)

Con esto ya podemos estimar el número de opciones para cada posicion, y sabemos que el número total de combinaciones es igual al producto entre los números de opciones para cada caso. El número total de combinaciones es:

C = 10*9*8*7*6*5*4*3*2*1 = 10!

Ahora si asumimos que no podemos diferenciar los libros de matemáticas, entonces no debemos contar sus permutaciones (si tenemos 4 libros de matemáticas, tenemos 4*3*2*1 permutaciones = 4! permutaciones). Debemos dividir al numero total de combinaciones por 4!.

Y lo mismo pasa para las 3! permutaciones de los libros de biología y las 3! permutaciones de los libros de religión.

Entonces el número total de combinaciones diferentes es:

`C = (10!)/(3!*4!*3!) = (10*9*8*7*6*5*4*3*2*1)/((3*2*1)*(4*3*2*1)*(3*2*1)) = 4,200`

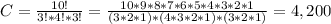
Hay 4200 diferentes formas de ordenar los libros.