Question

What is the lateral area of the pyramid

Answer 1

43.75 ft²

Explanation:

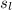`s_l` = (l√(w/2)² + h²) + (w√(l/2)² + h²)

l & w become 3.5, and h becomes 6.

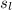`s_l` = (3.5√(3.5/2)² + 6²) + (3.5√(3.5/2)² + 6²)

Step 1:Because this is a square pyramid, what you see above essentially becomes what you see below.

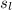`s_l` = 2(3.5√(3.5/2)² + 6²)

Step 2: Divide 3.5 by 2 to get 1.75.

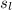`s_l` = 2(3.5√1.75² + 6²)

Step 3: Square both 1.75 and 6 to get 3.0625 and 36 respectively.

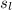`s_l` = 2(3.5√3.0625 + 36)

Step 4: Add 3.0625 and 36 to get 39.0625.

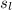`s_l` = 2(3.5√39.0625)

Step 5: The square root of 39.0625 is 6.25.

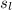`s_l` = 2(3.5 * 6.25)

Step 6: Multiply 3.5 by 6.25 to get 21.875.

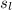`s_l` = 2(21.875)

Step 7: Multiply 2 by 21.875 to get 43.75.

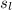`s_l` = 43.75 ft²

The lateral area of this pyramid is 43.75 ft².