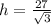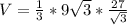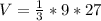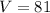Answer:
The volume of pyramid B is 81 cubic units
Explanation:
Given
Pyramid A
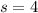 -- base sides
-- base sides
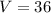 -- Volume
-- Volume
Pyramid B
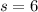 --- base sides
--- base sides
Required
Determine the volume of pyramid B [Missing from the question]
From the question, we understand that both pyramids are equilateral triangular pyramids.
The volume is calculated as:

Where B represents the area of the base equilateral triangle, and it is calculated as:

Where s represents the side lengths
First, we calculate the height of pyramid A
For Pyramid A, the base area is:

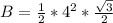

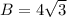
The height is calculated from:

This gives:
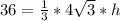
Make h the subject


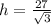
To calculate the volume of pyramid B, we make use of:

Since the heights of both pyramids are the same, we can make use of:
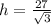
The base area B, is then calculated as:

Where
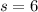
So:
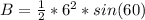
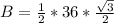
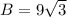
So:

Where
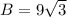 and
and