Question

Write an equation for the nth term of the arithmetic sequence. Then find a40.

1/4,1/2,3/4,1,...​

Answer 1

The nth term is:
`a_n = (1)/(4) + (1)/(4)(n-1)`

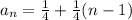
a40 = 10

Explanation:

Arithmetic sequence:

In an arithmetic sequence, the difference between consecutive terms is always the same, and this difference is called common difference.

The nth term of a sequence is given by:

`a_n = a_1 + (n-1)d`

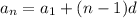
In which
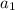`a_1` is the first term and d is the common difference.

1/4,1/2

This means that:

`d = (1)/(2) - (1)/(4) = (2)/(4) - (1)/(4) = (1)/(4)`

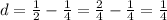
1/4

This means that
`a_1 = (1)/(4)`

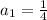
The nth term is:

`a_n = a_1 + (n-1)d`

`a_n = (1)/(4) + (1)/(4)(n-1)`

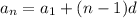
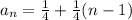
Then find a40.

`a_(40) = (1)/(4) + (1)/(4)(40-1) = (1)/(4) + (39)/(4) = (40)/(4) = 10`

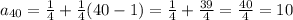
So

a40 = 10