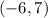Question

Place the quadratic y=2x^2+24x+79 into vertex form by using the method of completing the square and then state the coordinates of its vertex.

Answer 1

`y=2(x+6)^2+7`

`(-6,7)`

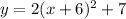
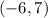
Explanation:

`y=2x^2+24x+79`

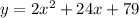
Completing the square is a process of converting a quadratic equation in standard form into vertex form.

The first step in completing the square is grouping the quadratic and linear terms of the quadratic equation.

`y=(2x^2+24x)+79`

Factor out the coefficient of the quadratic term,

`y=2(x^2+12x)+79`

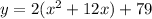
Now complete the square, add a term to make the grouped part of the equation a complete square, then balance the equation.

`y=2(x^2+12x+36-36)+79`

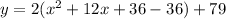
Simplify,

`y=2(x^2+12x+36)+79+(2)(-36)`

`y=2(x+6)^2+79-72`

`y=2(x+6)^2+7`

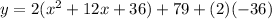
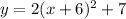
The x-coordinate of the vertex of the equation is equal to (-1) times the numerical part of the quadratic term, and the y-coordinate is equal to the constant.

`(-6,7)`