Question

If x = 1, y = 7, and z = 15, determine a number that when added to x, y, and z yields consecutive terms of a geometric sequence. What are the first three terms in the geometric sequence? 3

Answer 1

Given:

`x = 1, y = 7,z = 15`

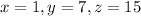
A number is added to x, y, and z yields consecutive terms of a geometric sequence.

To find:

The number which is added to x, y, and z, then find the first three terms in the geometric sequence.

Solution:

Let the unknown number be k.

After adding k to x, y, and z, we get

`x = 1+k, y = 7+k,z = 15+k`

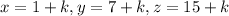
These are the consecutive terms of a geometric sequence. So,

`(7+k)^2=(1+k)(15+k)`

`49+14k+k^2=15+k+15k+k^2`

`49+14k=15+16k`

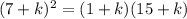
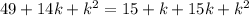
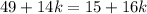
Isolate the variable terms.

`49-15=16k-14k`

`34=2k`

`(34)/(2)=k`

`17=k`

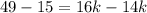
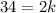
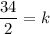
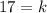
The unknown number is 17.

Now,

`x=1+k`

`x=1+17`

`x=18`

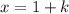
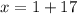
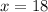
Similarly,

`y=7+k`

`y=7+17`

`y=24`

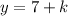
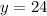
And

`z=15+k`

`z=15+17`

`z=32`

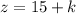
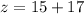
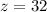
Therefore, the three terms in the geometric sequence are 18, 24, 32.