Question

You need to know how far you are away from the lighthouse.

You use a range finder to find the distance from the sailboat to the lighthouse light is 245 yards.
For angle B, chose an angle measure between 25° and 45°: __________
Based on the above information, find the distance from the sailboat to the island where the lighthouse is located.

Answer 1

The distance from the sailboat to the island where the lighthouse is located is approximately 212.2 yards

Explanation:

The distance between the sailboat and the lighthouse is found using trigonometric ratios as follows;

The given parameters are;

The distance from the sailboat to the lighthouse's light = 245 yards

The angle of elevation of angle B = An angle chosen between 25° and 45°

For simplicity, we chose, B = 30°

A right triangle formed with the height of the light house and the horizontal distance of the sailboat from the lighthouse as legs and angle B is the angle adjacent to the horizontal distance of sailboat from the light house

The hypotenuse length = The distance from the sailboat to the lighthouse's light = 245 yards

By trigonometric ratio, in the we have;

`cos\angle B = (Adjacent\ leg \ length)/(Hypotenuse \ length)`

The adjacent leg length = The horizontal distance of sailboat from the light house

`\therefore cos (30^(\circ)) = (The \ horizontal \ distance \ between \ the \ sailboat \ and \ the \ lighthouse )/(245 \ yards)`

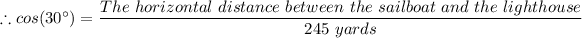
The horizontal distance between the sailboat and the light house = 245 × cos(30°) ≈ 212.176223927

Therefore;

The horizontal distance between the sailboat and the lighthouse ≈ 212.2 yards

Therefore, the distance from the sailboat to the island where the lighthouse is located ≈ 212.2 yards.