Question

LOT OF POINTS

approximate the solutions to this system.

y = 3x2 + x − 6

y = x − 4

Round your answers to the nearest hundredth.

Answer 1

(x1,y1) = (0.82, - 3.18)

(x2,y2) = (-0.82, -4.82)

Explanation:

Plato gang

Answer 2

`\displaystyle ( x_(1),y_(1)) = (0.82, - 3.18) \\ ( x_(2),y_(2)) = ( - 0.82, - 4.82)`

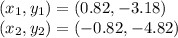
Explanation:

we are given a system of quadratic and linear equation

we want to figure out x and y

in other words the coordinates where the linear function intercept quadrilateral function

to do so

you can use substitution method

since y equals to both equation so substitute:

`\displaystyle {3x}^(2) + x - 6 = x - 4`

move right hand side expression to left hand side and change its sign so there's only 0 left on the left hand side:

`\displaystyle {3x}^(2) + x - 6 - x + 4= 0`

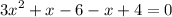
simplify addition:

`\displaystyle {3x}^(2) -2=0`

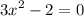
add 2 to both sides:

`\displaystyle {3x}^(2) = 2`

divide both sides by 3

`\displaystyle \frac{ {3x}^(2) }{3} = (2)/(3)`

`\displaystyle {x}^(2) = (2)/(3)`

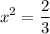
square root both sides:

`\displaystyle {x} = \sqrt{(2)/(3) } \\ x = ( √(2) )/( √(3) )`

rationalise the denominator by multiplying √3/√3:

`\displaystyle x = \pm( √(6) )/(3) = \pm0.82`

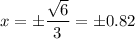
now let's figure out y

substitute the value of x to the linear equation:

`y = \pm0.82 - 4`

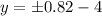
when positive

`y = - 3.18`

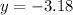
when negative

`y = - 4.82`