Question

Regular hexagon ABCDEF is inscribed in circle X and has an apothem that is 6√3 inches long. Use the length of the apothem to calculate the exact length of the radius and the perimeter of regular hexagon ABCDEF. In your final answer, include your calculations.

Answer 1

Answer: radius = 12, perimeter = 72

Explanation:

We know that in 30-60-90 right triangles, the hypotenuse is exactly twice the length of the short leg and the long leg is the short leg times √3.

so therefore, if the long leg (apothem) is equal to 6√3, the short leg is equal to 6

long leg = 6√3

long leg = short leg √3

short leg = 6

hypotenuse (radius) = 2(short leg)

hypotenuse (radius) = 2(6)

hypotenuse (radius) = 12

The radius of hexagon ABCDEF = 12 inches

Perimeter = r (sides)

Perimeter = r (6)

Perimeter = 12 (6)

Perimeter = 72

The perimeter of hexagon ABCDEF = 72 inches

Answer 2

Part A

`The \ circumradius, \ R = (a)/(cos \left((\pi)/(n) \right))`

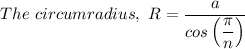
Plugging in the given values we get;

`The \ circumradius, \ R = (6 \cdot √(3) )/(cos \left((\pi)/(6) \right)) = (6 \cdot √(3) )/(\left((√(3) )/(2) \right)) = 6 \cdot √(3) * (2)/(√(3) ) = 12`

R = 12 inches

The radius of the circumscribing circle is 12 inches

Part B

The length of each side of the hexagon, 's', is;

`s = a * 2 * tan \left((\pi)/(n) \right)`

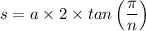
Therefore;

`s = 6 \cdot √(3) * 2 * tan \left((\pi)/(6) \right) = 6 \cdot √(3) * 2 * \left((1)/(√(3) ) \right) = 12`

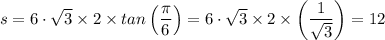
s = 12 inches

The perimeter, P = n × s = 6 × 12 = 72 inches

The perimeter of the hexagon is 72 inches

Explanation:

The given parameters of the regular hexagon are;

The length of the apothem of the regular hexagon, a = 6·√3 inches

The relationship between the apothem, 'a', and the circumradius, 'R', is given as follows;

`a = R \cdot cos \left((\pi)/(n) \right)`

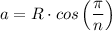
Where;

n = The number of sides of the regular polygon = 6 for a hexagon

'a = 6·√3 inches', and 'R' are the apothem and the circumradius respectively;

Part A

Therefore, we have;

`The \ circumradius, \ R = (a)/(cos \left((\pi)/(n) \right))`

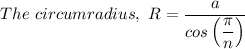
Plugging in the values gives;

`The \ circumradius, \ R = (6 \cdot √(3) )/(cos \left((\pi)/(6) \right)) = (6 \cdot √(3) )/(\left((√(3) )/(2) \right)) = 6 \cdot √(3) * (2)/(√(3) ) = 12`

The circumradius, R = 12 inches

Part B

The length of each side of the hexagon, 's', is given as follows;

`s = a * 2 * tan \left((\pi)/(n) \right)`

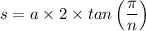
Therefore, we get;

`s = 6 \cdot √(3) * 2 * tan \left((\pi)/(6) \right) = 6 \cdot √(3) * 2 * \left((1)/(√(3) ) \right) = 12`

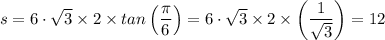
The length of each side of the hexagon, s = 12 inches

The perimeter of the hexagon, P = n × s = 6 × 12 = 72 inches

The perimeter of the hexagon = 72 inches