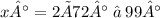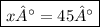Answer:

Explanation:
When two chords intersect at a point in a circle, they form arcs, along with angles at the intersection point.
To determine the angle of the arc, we must apply this geometric rule:
 .
.
Since we are looking for one of the arcs, we can rearrange this formula to solve for the first arc.
 →
→
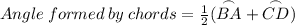 →
→
 →
→
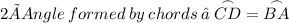
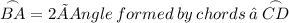
[Given]
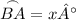
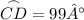
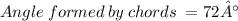
→
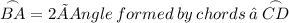
→