Question

Express the area of the entire rectangle.
Your answer should be a polynomial in standard form.

Answer 1

Area= height x width = (x + 6) (x+ 2) = x^2 + 2x + 6x + 12= x^2 + 8x + 12

Answer 2

The area of the entire rectangle is given by the polynomial
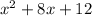`\(x^2 + 8x + 12\)` in standard form.

The area (A) of a rectangle is given by the formula
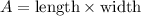`\(A = \text{length} * \text{width}\)`. In this case, the length is x + 6 and the width is x + 2. Therefore, the area (A) can be expressed as:

A = (x + 6)(x + 2)

Now, use the distributive property to expand the expression:

`\[ A = x \cdot (x + 2) + 6 \cdot (x + 2) \]`

`\[ A = x^2 + 2x + 6x + 12 \]`

Combine like terms:

`\[ A = x^2 + 8x + 12 \]`

So, the area of the entire rectangle is given by the polynomial
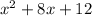`\(x^2 + 8x + 12\)` in standard form.