Question

The time between arrivals of small aircraft at a county airport is exponentially distributed with a mean of one hour. (a) What is the probability that more than three aircraft arrive within an hour? (b) If 30 separate one-hour intervals are chosen, what is the probability that no interval contains more than three arrivals?(c) Determine the length of an interval of time (in hours) such that the probability that no arrivals occur during the interval is 0.10.

Answer 1

(a) The probability that more than three arrive in one hour is approximately 0.018988

(b) The probability that no interval contains more than 3 arrivals in 30 separate one-hour intervals is approximately 0.56264

(c) The length of time such that the probability of no arrival is 0.1 is approximately 2.30259 hours

Explanation:

The distribution of the arrival time of a small aircraft = Exponential distribution

The mean arrival time, μ = 1 hour

The pdf of a exponential distribution, f(x) = λ·e^(-λ·x)

The mean, μ = 1/λ

∴ 1 = 1/λ

λ = 1 hour

∴ For the exponential distribution, f(x) = 1·e^(-x)

(a) The Poisson probability is given as follows;

`P(X = k) = (\lambda^k * e^(-k))/(k!)`

The probability for more than 3 is given as follows;

`P(X > 3) = 1 - (1^0 * e^(-1))/(0!) - (1^1 * e^(-1))/(1!) - (1^2 * e^(-1))/(2!) - (1^3 * e^(-1))/(3!) \approx 0.018988`

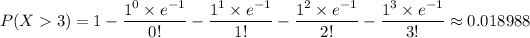
(b) P(X ≤ 3) for 30 1 hour intervals = P(X ≤ 3)³⁰ = (1 - 0.018988)³⁰ ≈ 0.56264

(c) When the probability that no arrival occurs is 0.1, we have;

0.1 P(X > x) = f(x) = 1·e^(-x) = e^(-x)

-x·ln(e) = ln(0.1)

∴ x = -㏑(0.1) ≈ 2.30259

The length of time such that the probability that no arrival occur during the interval is 0.1, x ≈ 2.30259 hours.