Answer:
(3, 0 )
Explanation:
Given a parabola in standard form
y = ax² + bx + c (a ≠ 0 )
Then the x- coordinate of the vertex is
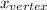 = -
= -
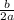
y = 5x² - 30x + 45 ← is in standard form
with a = 5, b = - 30 , then
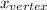 = -
= -
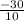 = 3
= 3
Substitute x = 3 into the function for corresponding value of y
y = 5(3)² - 30(3) + 45 = 45 - 90 + 45 = 0
vertex = (3, 0 )