Answer:
(x-2)²+(y-3)²=5².
Explanation:
1. the equation of line through points (5;7) and (2;-2) is:
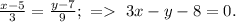
2. to find the equation of the line, which is perpendicular to the line 3x-y-8=0:
the vector (3;-1) is perpendicular to the line 3x-y-8=0 and it is the vector-pointer for the requred line, and if |n₁|*|n₂|=0 (where n₁ is normal vector to the line 3x-y-8=0 and n₂ is normal vector to the required line), then 3*x-1*y=0 (where 'x' and 'y' any numbers). x=1; y=3, then n₂(1;3), then the required line is x+3y+C=0, where C - is unknown number.
3. to find the equation of the line, which is perpendicular to the line 3x-y-8=0 and passes through the middle point of (5;7) and (2;-2):
middle point is (7/2;5/2), then after substitution of coordinates of the middle point into the equation x+3y+C=0 it will be 3.5+3*2.5+C=0, ⇒ C= -11.
the required equation is x+3y-11=0
4. to calculate the intersection point of x+3y-11=0 and 2x-y=1:
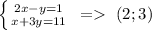
the point (2;3) is the centre of the required circle.
5. to calculate the radius² of the required circle:
r²=(5-2)²+(7-3)² or r²=(2-2)²+(2+3)², then r²=5².
6. if the centre of the required circle is (2;3) and its r²=25, then it is possible to make up the equiation of the circle:
(x-2)²+(y-3)²=5².