Answer:
A. The angular acceleration of the disk is -1.047 radians per square second.
B. The disk turns 4.715 radians while stopping.
C. The disk did 0.750 revolutions while stopping.
Step-by-step explanation:
A. In this case, the disk is deceleration at a constant rate. Hence, the angular acceleration experimented by the object (
 ), in radians per square second, can be found by means of this kinematic expression:
), in radians per square second, can be found by means of this kinematic expression:
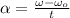 (1)
(1)
Where:
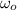 - Initial angular speed, in radians per second.
- Initial angular speed, in radians per second.
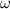 - Final angular speed, in radians per second.
- Final angular speed, in radians per second.
 - Time, in seconds.
- Time, in seconds.
If we know that
 ,
,
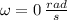 and
and
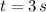 , then the angular acceleration of the disk is:
, then the angular acceleration of the disk is:
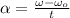
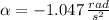
The angular acceleration of the disk is -1.047 radians per square second.
B. The change in position of the disk (
 ), in radians, is determined by the following kinematic formula:
), in radians, is determined by the following kinematic formula:
 (2)
(2)
If we know that
 ,
,
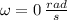 and
and
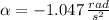 , then the change in position is:
, then the change in position is:

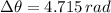
The disk turns 4.715 radians while stopping.
C. A revolution equals 2π radians, then, then number of revolutions done by the disk while stopping is found by simple rule of three:

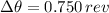
The disk did 0.750 revolutions while stopping.