Answer:
The point will travel a distance of 15708 centimeters in 30 seconds of rotation.
Step-by-step explanation:
In this case, we see a disk rotating at constant rate, the travelled distance of a point on the outside rim (
 ), in centimeters, is determined by using this expression:
), in centimeters, is determined by using this expression:
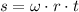 (1)
(1)
Where:
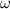 - Angular speed, in radians per second.
- Angular speed, in radians per second.
 - Radius of the disk, in centimeters.
- Radius of the disk, in centimeters.
 - Time, in seconds.
- Time, in seconds.
If we know that
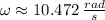 ,
,
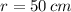 and
and
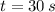 , then the travelled distance of the point is:
, then the travelled distance of the point is:
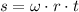
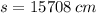
The point will travel a distance of 15708 centimeters in 30 seconds of rotation.