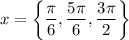Answer:
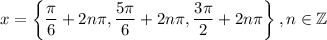
Explanation:
We are given the equation:

And we want to find all solutions for x.
First, we should put the equation into terms of only one trigonometric ratio.
Since we are given cos²(x), we can turn this into sine. Recall the Pythagorean Identity which states:
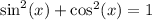
Therefore:
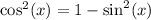
By substitution:
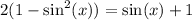
Distribute:
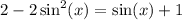
Isolate the equation:
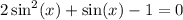
We can factor:
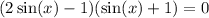
Zero Product Property:

Solve for each case:

We can use the unit circle.
sin(x) = 1/2 for every π/6 and 5π/6. So, it will continue every 2π.
sin(x) = -1 every 3π/2. And this will also continue every 2π.
Hence, our solutions are:
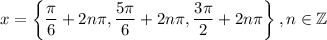
Note:
If you only need the solutions within the interval [0, 2π), then it is: