Answer:
The area of the sector (shaded section) is 29.51
 .
.
Explanation:
Area of a sector = (θ ÷ 360)

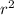
where θ is the central angle of the sector, and r is the radius of the circle.
From the diagram give, diameter of the circle is 26 m. So that;
r =
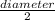
=
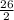 = 13 m
= 13 m
θ = 360 - (180 + 160)
= 360 - 340
=
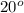
Thus,
area of the given sector =
 x
x
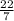 x
x
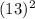
=
 x x
x x
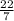 x 169
x 169
= 29.5079
The area of the sector (shaded section) is 29.51
 .
.