Question

Driving instructors Mr. Adams and Mr. Bateman teach class independently of each other. Among Mr. Adams’s students, 68% pass the driving test on the first try, while 74% of Mr. Bateman’s students pass the driving test on the first try. Suppose there are 40 students in Mr. Adams’s class and 50 students in Mr. Bateman’s class. Let A = the proportion of students who pass the driving test on the first try from Mr. Adams’s class and B = the proportion of students who pass the driving test on the first try from Mr. Bateman’s class. What is the probability that Mr. Bateman’s class has more students who pass on the first try?

Find the z-table here.

0.266
0.547
0.734
0.765

Answer 1

0.734, c

Explanation:

Answer 2

0.989 = 98.9% probability that Mr. Bateman’s class has more students who pass on the first try

Explanation:

To solve this question, we need to understand the normal probability distribution, the binomial approximation to the normal and subtraction of normal distributions.

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(X) = np`

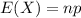
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

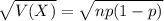
Subtraction of normal distributions:

When two normal variables are subtracted, the mean is the subtraction of the means while the standard deviation is the square root of the sum of the variances.

Among Mr. Adams’s students, 68% pass the driving test on the first try. Sample of 40.

This means that
`p = 0.68, n = 40`.

`\mu_A = np = 40*0.64 = 27.2`

`s_A = √(40*0.68*0.32) = 2.95`

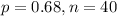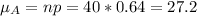
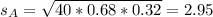
74% of Mr. Bateman’s students pass the driving test on the first try. Sample of 50:

`p = 0.74, n = 50`

`\mu_B = np = 50*0.74 = 37`

`s_B = √(50*0.74*0.26) = 3.1016`

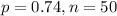
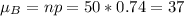
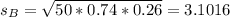
What is the probability that Mr. Bateman’s class has more students who pass on the first try?

This is the probability that B - A is greater than 0.

Distribution B - A:

Mean:

`\mu = \mu_B - \mu_A = 37 - 27.2 = 9.8`

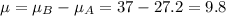
Standard deviation:

`\sigma = √(s_A^2 + s_B^2) = √(2.95^2 + 3.1016^2) = 4.28`

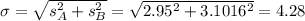
Probability of being larger than 0:

1 subtracted by the pvalue of Z when X = 0. So

`Z = (X - \mu)/(\sigma)`

`Z = (0 - 9.8)/(4.28)`

`Z = -2.29`

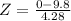
`Z = -2.29` has a pvalue of 0.011

1 - 0.011 = 0.989

0.989 = 98.9% probability that Mr. Bateman’s class has more students who pass on the first try