Answer:
A. F(x)is an even function so both ends of the graph go in the same direction.
D. The leading coefficient is negative so the left end of the graph goes down.
Explanation:
Even function:
For every value of x, f(x) = f(-x)
In this question:
We are given the following function:
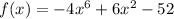
Testing if it is even:
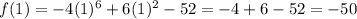
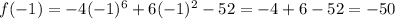
Since f(1) = f(-1), it is even.
Since it is even, both ends of the graph go in the same direction, so option A is correct, while option B is wrong.
Options C and D:
The leading coefficient, is -4(which multiplies x with the highest exponent). Since it is negative, it goes to negative infinity as x increases, that is, the left end goes down, and option D is correct while C is not.