Question

Find the value of x and y in the parallelogram below.

Answer 1

x=7

y=-17

Explanation:

Lets do 10x-7. Basically it will be equal to 63, so the equation will be 10x-7=63

to find x we need to add 63+7=70 and put 10x with an equal sign which is 70=10x

7=x because 70/10=7.

in a simple way it is

10x-7=63

10x=7+63=70

10x=70

x=7

Lets do -5y+3. It is equal to 88.

so it will be

-5y+3=88

-5y=88-3=85

-5y=85

y=-17

Answer 2

`\Longrightarrow: \boxed{\sf{x=7, \ y=-17}}`

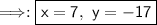
Explanation:

To find the value of x and y in the parallelogram, you have to isolate it on one side of the equation.

10x-7=63

First, add by 7 from both sides.

10x-7+7=63+7

Solve.

Add the numbers from left to right.

63+7=70

10x=70

Then, you divide by 10 from both sides.

10x/10=70/10

Solve.

Divide these numbers goes from left to right.

70/10=7

`\Longrightarrow: \boxed{\sf{x=7}}`

-5y+3=88

Subtract by 3 from both sides.

-5y+3-3=88-3

Solve.

Subtract the numbers from left to right.

88-3=85

-5y=85

Divide by -5 from both sides.

-5y/-5=85/-5

Solve.

Divide the numbers from left to right.

85/-5=-17

`\Longrightarrow: \boxed{\sf{y=-17}}`

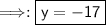
• Therefore, the correct answer is x=7 and y=-17.

I hope this helps. Let me know if you have any questions.