Question

Start with x2 - 6x + 8 = 0 and complete the square, what is the equivalent equation?

es -))
A)
(x + 3)2 = 1
B)
(x+3)2 = 9
C)
(x - 3)2 = 1
D)
(x-3)=9

Answer 1

To complete the square for the given equation
`x^2- 6x + 8 = 0`, move the constant term, add the square of half of the coefficient of the x-term, and simplify to obtain C.
`(x - 3)^2 = 1.`

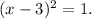
Step-by-step explanation:

To complete the square for the equation x² - 6x + 8 = 0, follow these steps:

Move the constant term to the right side of the equation: x² - 6x = -8

Take half of the coefficient of the x-term, square it, and add it to both sides of the equation:

`x^2 - 6x + (-6/2)^2`

`= -8 + (-6/2)^2`

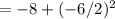
Simplify both sides of the equation:
`(x - 3)^2 = 1`

Therefore, the equivalent equation is
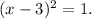`(x - 3)^2 = 1.` which is option A.