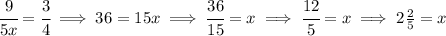a whole is always fraction wise "1", whether is 5/5 or 4/4 or 1,000,000/1,000,000 it'd round up to "1", just 1 whole.
we know how much 3/4 of his land is, so the "whole land" will be in quarters, 4/4 or namely "1".
let's firstly convert the mixed fraction to improper fraction and then proceed.
![\stackrel{mixed}{1(4)/(5)}\implies \cfrac{1\cdot 5+4}{5}\implies \stackrel{improper}{\cfrac{9}{5}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{ccll} acres&whole\\ \cline{1-2} (9)/(5)&(3)/(4)\\[1em] x&(4)/(4) \end{array}\implies \cfrac{~~(9)/(5) ~~}{x}=\cfrac{~~ (3)/(4)~~}{(4)/(4)}\implies \cfrac{~~(9)/(5) ~~}{(x)/(1)}=\cfrac{~~ (3)/(4)~~}{1}\implies \cfrac{9}{5}\cdot \cfrac{1}{x}=\cfrac{3}{4}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/ysndfjmsa15lts5ibnwx.png)