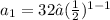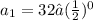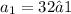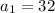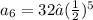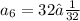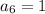Answer:
32, 16, 8, 4, 2, 1
Step-by-step explanation:
The geometric mean can be represented by
![\sqrt[n]{x_(1) • x_(2) • x_(3) • .. x_(n)}](https://img.qammunity.org/2022/formulas/mathematics/college/v7rlfyre43v1sjrt48jfz2lcp6r8heq9r2.png) .
.
Which is the mean of the product of n numbers, used to find the average of a geometric progression.
Don't get confused by geometric mean, it is only asking you about the next numbers in the geometric sequence given the first and sixth term.
The explicit rule for a geometric sequence can be modeled by:
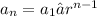
Where
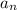 is the nth term,
is the nth term,
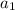 is the first term in the sequence, n is the term number, and r is the common ratio.
is the first term in the sequence, n is the term number, and r is the common ratio.
Since we already know the first term,
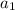 will simply be 32.
will simply be 32.
Since we know it's geometric, there will be an exponential relationship, which means that we will use the geometric mean to find the common ratio.
There are 6 total terms, r is raised to the n – 1 so 6 – 1 = 5, and that will be the degree of this root.
![\sqrt[5]{(a_(6))/(a_(1))}](https://img.qammunity.org/2022/formulas/mathematics/college/r1owdpshl8fei8yxydozdkd60z8209uxeb.png) =
=
![\sqrt[5]{(1)/(32)}](https://img.qammunity.org/2022/formulas/mathematics/college/umiftr0elepzt829itb3kaweye5kjgfvmq.png) =
=
 .
.
Therefore:
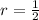 .
.
Using all the information we have, we can find the explicit rule:
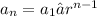
-
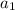 = 32
= 32
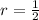
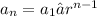 →
→
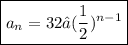
________________________________
We can test that this works by substituting the number location of the term you want to find.
For instance: