Answer:

Explanation:
Given

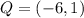
Reflection over:

Required
Determine the coordinates of P'
From the given coordinates, the y coordinates of P is 6 and the line of reflection is at y = 2
Since we are to reflect over y = 2, only the y coordinate of P will be affected.
The idea behind reflecting a point over a line is to have an equal distance between [the original point & the line of reflection] and [the new point & the line of reflection]
So, what to do is:
First, calculate the difference between the y coordinates of P and the line of reflection.
The y coordinate of P is 6 and the line of reflection is at y = 2.
So, the difference is: 6 -2 = 4
Next, subtract the calculated difference from the line of reflection to get the y coordinate of P'
y coordinate of P' = 2 - 4 = -2
Hence, the coordinate of P' is: (1,-2)