Question

Use the following diagram to find the angle measures of the triangle, rounded to the nearest degree.

​ m∠A=
m∠B=
m∠C=

Answer 1

m∠A = 30°

m∠B = 80°

m∠C = 70°

Explanation:

By applying cosine rule in the given triangle,

b² = a² + c² - 2ac[cos(∠B)]

From the given triangle,

a = 14 m

b = 28 m

c = 24 m

(28)² = (14)² + (24)² - 2(14)(24)cos(B)

784 = 196 + 576 - 672cos(∠B)

cos(∠B) = 0.1786

∠B =
`\text{cos}^(-1)(0.1786)`

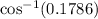
∠B = 79.71°

∠B = 80°

By applying sine rule in the given triangle,

`\frac{\text{sinA}}{a}= \frac{\text{sinB}}{b}= \frac{\text{sinC}}{c}`

`\frac{\text{sinA}}{14}= \frac{\text{sin(79.71)}}{28}= \frac{\text{sinC}}{24}`

`\frac{\text{sinA}}{14}= \frac{\text{sin(79.71)}}{28}`

`\text{sinA}= \frac{\text{sin(79.71)}* 14}{28}`

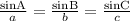
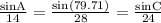
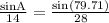
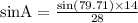
sinA = 0.491958

A = 29.47°

A ≈ 30°

By applying triangle sum theorem,

m∠A + m∠B + m∠C = 180°

30° + 80° + m∠C = 180°

m∠C = 70°