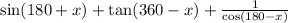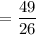Question

If
`tan (x) = (5)/(12)`

and x is in third quarter
find :

`sin(180+x) + tan(360-x) + (1)/(cos(180-x))`
Please i want step by step not only the answer

Answer 1

Step-by-step explanation:

First, we need to find the values of the sine and cosine of x knowing the value of tan x and x being in the 3rd quadrant. Since tan x = 5/12, using Pythagorean theorem, we know that

`\sin x = -(5)/(13)\;\;\text{and}\;\;\cos x = -(12)/(13)`

Note that both sine and cosine are negative because x is in the 3rd quadrant.

Recall the addition identities listed below:

`\sin(\alpha + \beta) = \sin\alpha\sin\beta + \cos\alpha\cos\beta`

`\Rightarrow \sin(180+x) = \sin180\sin x + \cos180\cos x`

`\;\;\;\;\;\;= -\sin x = (5)/(13)`

`\cos(\alpha - \beta) = \cos\alpha \cos\beta + \sin\alpha \sin\beta`

`\Rightarrow \cos(180 - x) = \cos180\cos x + \sin180\sin x`

`\;\;\;\;\;\;=-\cos x = (12)/(13)`

`\tan(\alpha - \beta) = (\tan\alpha - \tan\beta)/(1 + \tan\alpha\tan\beta)`

`\Rightarrow \tan(360 - x) = (\tan 360 - \tan x)/(1 + \tan 360 \tan x)`

`\;\;\;\;\;\;= -\tan x = -(5)/(12)`

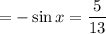
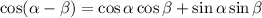
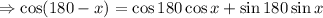
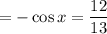
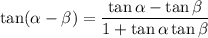
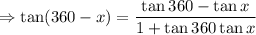
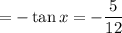
Therefore, the expression reduces to

`\sin(180+x) + \tan(360-x) + (1)/(\cos(180-x))`

`\;\;\;\;\;= \left((5)/(13)\right) + \left((5)/(12)\right) + (1)/(\left((12)/(13)\right))`

`\;\;\;\;\;= (49)/(26)`