Question

G(x)=3x+2 and h(x)=ax+B

where a and b are constants
h(4)=22
g^-1(14)=h(1)
find the value of a and the value of b

Answer 1

a=6

b=-2

Explanation:

You can use the hint provided on the mathswatch question page, I've attached it below

step 1

h(4) = ax+b = (ax4)+b = 4a+b

it is given in the question that h(4)=22, therefore 4a+b=22

step 2

work out the equation for inverse g

g^-1(x) =
`(x-2)/(3)`

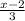
step 3

input 14 into the equation in place of x to find g^-1(x)

`(x-2)/(3) =(14-2)/(3) =(12)/(3) =4`

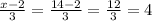
so, g(x)^-1=4

step 4

find h(1):

h(1) = (ax1)+b = a+b

so, h(1)=a+b

step 5

a+b=4 (as it is given in the question that g^-1(14) is equal to h(1))

step 6

Now you have two simultaneous equations:

4a+b=22

a+b=4

then, solve for a:

4a+b=22

- a+b=4

3a=18

a=6

then, input answer for a into either equation (I've gone with the a+b=4 equation):

6+b=4

-6 - 6

b=-2

(p.s i know this is very late but hope it helps someone)