Question

Which equation is y = (x + 3)2 + (x + 4)2 rewritten in vertex form?

y = 2 (x + seven-halves) squared minus one-fourth
y = 2 (x + seven-halves) squared minus one-half
y = 2(x + 7)2 – 73
y = (x + 7)2 – 24

Answer 1

b

Explanation:

edge 2021

Answer 2

y = 2 (x + seven-halves) squared minus one-fourth [y =
`(x + (7)/(2) )^(2) - (1)/(4)` ]

Explanation:

We know that,

vertex form is y = a(x-h)² + k

vertex is (h, k)

Now,

Given that the equation is -

y = (x+3)² + (x+4)²

= x² + 3² + 2×3×x + x² + 4² + 2×4×x

= x² + 9 + 6x + x² + 16 + 8x

= 2x² + 14x + 25

=
`x^(2) + 7x + (25)/(2)`

=
`x^(2) + 7x + (25)/(2) + (49)/(4) - (49)/(4)`

=
`(x + (7)/(2) )^(2) + (25)/(2) - (49)/(4)`

=
`(x + (7)/(2) )^(2) - (1)/(4)`

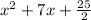
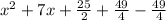
∴ we get

The vertex form is -

y =
`(x + (7)/(2) )^(2) - (1)/(4)`

So,

The correct option is - y = 2 (x + seven-halves) squared minus one-fourth (y =
`(x + (7)/(2) )^(2) - (1)/(4)` )