
This is a disguised quadratic equation. To solve it, we must first multiply each term by x to get rid of the fraction:
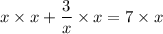
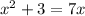
Now, we could solve this equation like a normal quadratic. Move all terms to the left side of the equation:
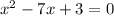
To solve for x, we could use the quadratic formula:
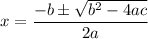 where the given equation is
where the given equation is

Given
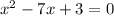 , we know that:
, we know that:
a = 1
b = -7
c = 3
Plug in a, b and c:

Therefore, the two solutions for x are
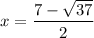 and
and
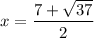 .
.
I hope this helps!