Answer:

Explanation:
we are given a limit
and we want to simplify it
notice that, the numerator is in a sequence of sum of natural number
recall that,
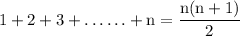
so substitute:
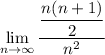
now recall L'Hôpital's rule
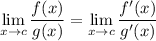
first simplify the complex fraction:
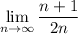
apply L'Hôpital's rule:
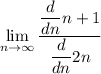
simplify:

and we are done: