Answer:
![Domain: [0,17]](https://img.qammunity.org/2022/formulas/mathematics/college/6a600hcsd8jxyfmpneoyilsuw1tfg87l86.png)
![Range:[0,544]](https://img.qammunity.org/2022/formulas/mathematics/college/y2vzkbzjee7cno1ay2t07q3j8ujd60meg5.png)
Explanation:
Given
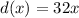
Maximum gallon = 17
Required
Determine the domain and range --- This completes the question
If the maximum is 17 (i.e. at full capacity) then the minimum is 0 (i.e. when empty)
So, the domain is:
![Domain: [0,17]](https://img.qammunity.org/2022/formulas/mathematics/college/6a600hcsd8jxyfmpneoyilsuw1tfg87l86.png)
To calculate the range, substitute 0 and 17 for x in
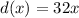
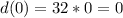
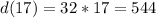
So, the range is:
![Range:[0,544]](https://img.qammunity.org/2022/formulas/mathematics/college/y2vzkbzjee7cno1ay2t07q3j8ujd60meg5.png)