This is a classic case of 'velocity components.'
Imagine a vector for velocity. Now, consider that this vector could be the hypotenuse of a right triangle, with two other sides going along the x and y-axis. These sides of the triangle will have values, and adding them up using the pythagorean theorem will prove that the sum of their squares equals the square of the original vector.
Well, okay, that's nice and all, you may be saying - but how do we solve the actual question?
Let's apply this thought to the question. This vector can have both an x component and y component (essentially, parts of the vector that travel along the x and y-axis).
Now, what could these components be? We know that the stone is thrown perfectly horizontally, meaning that the x-component is quite literally the velocity.
How about the y-component? Since it's thrown at a perfect horizontal, there isn't really any vertical velocity whatsoever. There's only horizontal velocity.
"Great, fantastic! So, what's the importance of figuring out the horizontal and vertical velocities?"
When a stone is in free fall, it experiences a gravitational acceleration. This acceleration from gravity, though, only affects the vertical velocity. Since gravity is vertical as well, it's essentially impossible for the horizontal velocity to be changed at all.
This means that to solve the horizontal distance, we simply need to find the time it takes for the rock to hit the ground and multiply said time by the horizontal velocity.
Since the vertical velocity is the only thing changed by gravity, we can write out an equation that can solve for the time:
∆Y =
 t +
t +
 g
g
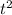
We know that initial vertical velocity is zero, so:
∆Y =
 t +
t +
 g
g
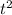
∆Y = 0t +
 g
g
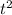
∆Y =
 g
g
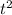
We need to solve for t, so let's isolate the variable. Multiply both sides by 2 to get rid of the fraction:
∆Y * 2 =
 g
g
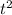 * 2
* 2
2∆Y = g
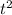
Divide both sides by g:
(2∆Y)/g =
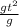
Square root both sides:
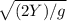 =
=
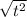
t =
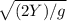
Input our values for Y and g (Y is the height of the cliff, and g is gravitational acceleration):
t =
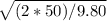
Solve:
t =
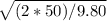
t = 3.194 (s)
Whew! That was a lot of steps to find the time! Now that we have the time, we can find the horizontal distance the rock travels:
∆x =
 t +
t +
 a
a
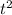
The horizontal velocity has no acceleration (gravity is vertical!), so:
∆x =
 t +
t +
 *0*
*0*
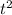
∆x =
 t
t
The horizontal velocity is 15 m/s, and the time is 3.194:
∆x =
 t
t
∆x = 15 * 3.194
∆x = 47.91 (m)
Since we rounded the time, it makes sense that our final answer's a little bit off to the options. The closest one is option B, which is only 0.6m off, a tiny difference that may have come from the test maker's use of '10 m/
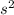 ' as the gravitational acceleration (while we stayed as accurate as possible with 9.80) as well as our rounding of the final time.
' as the gravitational acceleration (while we stayed as accurate as possible with 9.80) as well as our rounding of the final time.
Option B, the stone will have travelled 47.85 meters.
If you have any questions on how I got to the answer or if you're still confused on any topic I attempted to explain, just ask in the comments and I'll try to answer it to the best of my ability! Good luck!
- breezyツ