1 Answer

NiRUS · Answer 1 · 2022-10-19T20:24:14+0000

Answer:

(b)

Explanation:

Given

A roll of a six sided die

Required

Which of the options is true

A) P(Even) = 1/4 and P(Odd) = 3/4

In a die, we have:

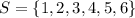$S = \{1,2,3,4,5,6\}$ -- sample space

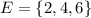$E = \{2,4,6\}$ --- Even

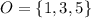$O = \{1,3,5\}$ -- Odd

The probability of even is the number of even sides over total.

i.e.

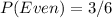
P(Even) = 3/6

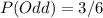
P(Odd) = 3/6

Hence, (a) is incorrect

(b) A) P(Even) = 1/2 and P(Odd) = 3/2

In (a), we have:

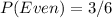
P(Even) = 3/6

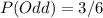
P(Odd) = 3/6

Simplify each

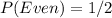
P(Even) = 1/2

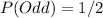
P(Odd) = 1/2

Hence (b) is true

Since (b) is true, (c) and (d) are false

Please log in or register to add a comment.