Question

Aiden invested $98,000 in an account paying an interest rate of 2 % compounded

continuously. Autumn invested $98,000 in an account paying an interest rate of 2%
compounded quarterly. After 11 years, how much more money would Autumn have in
her account than Aiden, to the nearest dollar?

Answer 1

5222

Explanation:

Answer 2

Aiden would have $67 more than Autumn.

Explanation:

Aiden compounded continuously, which uses the formula:
`P(t)=P_oe^r^t`

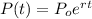
Plugging in what we know about Aiden's investment:
`P(11)=98000e^0^.^0^2^*^1^1`

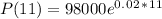
That gives us: 122115.5196

Autumn invested using regular compound interest, which has the formula:
`A=P(1+(r)/(t))^n^t`

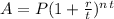
Since Autumn's investment is getting compounded quarterly, n=4 because it gets compounded 4 times a year.

Plug in Autumn's investment:
`A=98000(1+(0.02)/(4))^4^*^1^1`

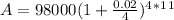
That gives us: 122048.5974

Now just subtract the two and round to the nearest dollar:

`122115.5196-122048.5974=66.92215187`

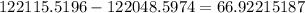
OR

$67. Aiden would have $67 more than Autumn after 11 years.