Answer:
The dolphin will be above the surface of the water for 2 seconds.
Explanation:
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
 .
.
This polynomial has roots
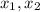 such that
such that
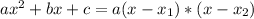 , given by the following formulas:
, given by the following formulas:

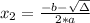
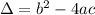
The height of the dolphin after t seconds is given by:
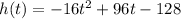
According to Micha's model, how long will the dolphin be above the surface of the water?
It stays above the surface of the water between the first and the second root. Initially, it is below water, when the first time for which
 it crosses the surface upwards, and then the second time for which
it crosses the surface upwards, and then the second time for which
 it crosses the surface downwards.
it crosses the surface downwards.
We have to find these roots. So
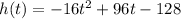
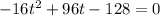
Multiplying by -16
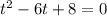
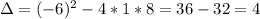
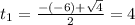

4 - 2 = 2
The dolphin will be above the surface of the water for 2 seconds.