Question

During peak systole, the heart delivers to the aorta a blood flow that has a velocity of 100cm/sec at a pressure of 120mmHg. The aortic root has a mean diameter of 25mm. Determine the force (Rz)acting on the aortic arch if the conditions at the outlet are a pressure of 110mmHg and a diameter of 21mm. The density of blood is 1050 kg/m3. Assume that aorta is rigid non-deformable and blood is incompressible and steady state. Ignore the weight of blood vessel and the weight of blood inside the blood vessel (i.e. body force is zero).

Answer 1

Given :

Velocity,
`$V_1 =100$` cm/sec

Pressure,
`$P_1 = 120 $` mm Hg

Then,
`$P_1 = \rho_1 g h$`

`$P_1 = 0.120 * 13.6 * 1000 * 9.81$`

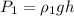
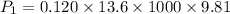
= 16.0092 kPa

`$P_2 = 110 $` mm Hg

`$P_2 = \rho_2 g h$`

`$= 0.110 * 13.6 * 1000 * 9.81$`

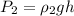
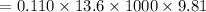
= 14.675 kPa

Then blood is incompressible,

`$A_1v_1=A_2v_2$`

`$(\pi)/(4)(25)^2* 100=(\pi)/(4)(21)^2* v_2$`

`$v_2=141.72 \ cm/s$`

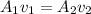
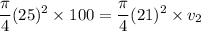
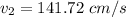
Then the linear momentum conservation fluid :

(Blood ) in y - direction

`$P_1A_1+ P_2A_2-F_g = m_2v_2-m_1v_1$`

`$m_1=m_2=P_1A_1v_1$`

`$=1.50 * (\pi)/(4)* (0.025)^2 * 1.00$`

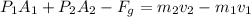
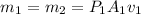
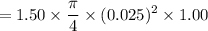
= 0.515 kg/ sec

Then the linear conservation of momentum of blood in y direction.

`$P_1A_1+ P_2A_2-F_g = m_2v_2-m_1v_1$`

`$16.0092 * 1000 * (\pi)/(4) * (0.025)^2+14.675 * 1000* (\pi)/(4)* (0.021)^2$`

`$-F_y=0.515(-1.4172-1)$`

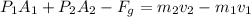
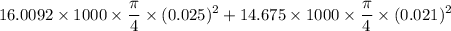
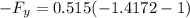
7.858+5.0828- Fy = 0.515(-2.4172)

Fy = 14.1856 N