Answer:
The surface area of Design A is smaller than the surface area of Design B.
The area of Design A is 94.65% of the Design B.
Explanation:
The area of a right cone is given by the sum of the circle area of the base and the lateral area:
 (1)
(1)
Where:
r: is the radius
L: is the slant height
The slant height is related to the height and to the radius by Pitagoras:
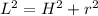
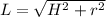 (2)
(2)
By entering equation (2) into (1) we have:
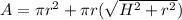
Now, let's find the area of the two cases.
Design A: height that is double the diameter of the base, H= 2D = 4r
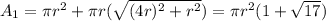
The volume of the cone is:

We can find "r":
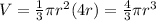
![r = \sqrt[3]{(3V)/(4\pi)} = \sqrt[3]{(3*1000)/(4\pi)} = 6.20 cm](https://img.qammunity.org/2022/formulas/mathematics/high-school/43605g0giy2xwmhsif4nuse6g2neh1h0wm.png)
The area is:
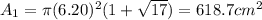
Design B: height that is triple the diameter of the base, H = 3D = 6r
The radius is:
![r = \sqrt[3]{(3V)/(6\pi)} = \sqrt[3]{(3*1000)/(6\pi)} = 5.42 cm](https://img.qammunity.org/2022/formulas/mathematics/high-school/hua46ljmpmr4maakihoim7mswihkmmsbk9.png)
The area is:
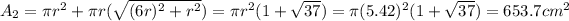
Hence, the surface area of Design A is smaller than the surface area of Design B.
The percent of the surface area of Design A is less than Design B by:
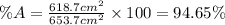
Therefore, the area of Design A is 94.65% of the Design B.
I hope it helps you!